NOTES

y=a(x-p)(x-g)
X Intersepts

• Solve for a
• Write a equation
• Leave in form y=a(x-p)(x-g)

y=ax^2+bx+c

• 3 pts/ 3 equations
• Solve the system for a,b,c
• Plug into equation y=ax^2+bx+c

y=a(x-h)^2+k
Vertex: (h,k)
Point: (x,y)

• Solve for a
• Use a,h,k
• to write an equation y=a(x-h)^2+k

Graphs !!!

Standard form of a quadratic equation.

y  =  x² + bx + c

Standard form of a parabolic equation.



y  =  a(x - h)²  + k

vertex (h, k)

• If you change a it makes the graph open up or down
  • Up when a is positive.
  • Down when a is negative.
  • Fractions (0 < a < 1) make the parabola wider.
  • Numbers (a > 1) make the graph narrower.

• Changing h, h is the number inside the ( ) that moves the parabola to the right or left.
  • you have to move it in the opposite direction.

 

• if you have (x + 2)² the graph moves two places to the left.
• if you have (x - 3)² the graph moves three places to the right.

• Changing k, k is the number outside the ( ) that moves the parabola up or down.

 

• if you have (x)² + 2 the graph moves up two places.
• if you have (x)² - 3 the graph moves down three places.

Z-Score

• Difference of two squares
  • a²- b² = (a + b)(a - b)
    •  x²-25= (x+5) (x-5)
    • x²-
• Trinomial perfect squares
  • a² + 2ab + b² = (a + b)(a + b) or (a + b)²
    • 3 examples
  • ^{a2 - 2ab + b2 = (a - b)(a - b) or (a - b)2}
    • 3 examples
• Difference of two cubes
  • a³ - b³
    • 3 - cube root 'em
    • 2 - square 'em
    • 1 - multiply and change
      • 3 examples
• Sum of two cubes
  • a³ + b³ 
    • 3 - cube root 'em
    • 2 - square 'em
    • 1 - multiply and change
      • 3 examples
• Binomial expansion
  • (a + b)³ = Use the pattern
  • (a + b)⁴ = Use the pattern

Zero Discriminant

• Zero Discriminant
• 1 real solution

Positive Discriminant

• Positive Discriminant, crosses the X- axis
• 2 real solutions

Negitive Discriminant

•  Positive Discriminant
• 2 real solutions

Quadrilaterals

Quadrilaterals

• four sides
• sum of the interior angles is 360 degrees

Kite

• 2 pair of congruent sides
• consective sides are not congruent

Parallelogram

• both pairs of oppisite sides are congruent
• both pairs of oppisite angles are congruent

Rectangles

• 4 right angles
• diagonals are congruent

Rhombus

• parellelogram with 4 congruent sides
• diagonals are perpendicular
• pair of oppisite angles

Square

• all sides are congruent
• angles are are congruent
•  diagonals intersect at 90 degrees

Trapizoid

• 1 pair of parellel sides

Points of Concurrency

Obtuse Triangle

Obtuse Triangle- One side is above 90 degreese.

Scalene Obtuse

Scalene obtuse- all angles are different and one angle is above 90 degreese.

Scalene acute

Scalene acute- all angles are different and 1 angle is above 90 degreese.

Isosceles obtuse

Two sides are congruent and one side is greater then 90 degrees.

Isosceles Acute

Two sides are congruent and one side is less then 90 degrees.

Acute Triangle

All three angles are different and all angles are less than 90.

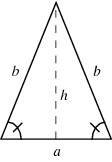
Isosceles Right Triangle

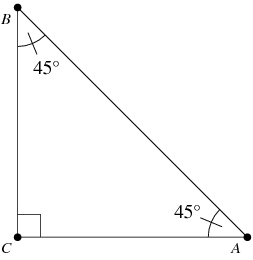
An isosceles right triangle has angles of 45 degrees, 45 degrees, and 90 degrees.

Isosceles triangle

A triangle with  two equal sides, and one side is greater than 90.

AAS

  
* Anlges BC and ED are congruent
* Angles AB and FE are congruent
* Angles AC and FD are congruent

SSS

* Angles AB and YX are congruent
* Angles BC  and YZ are congruent
* Angles CA and ZX are congruent